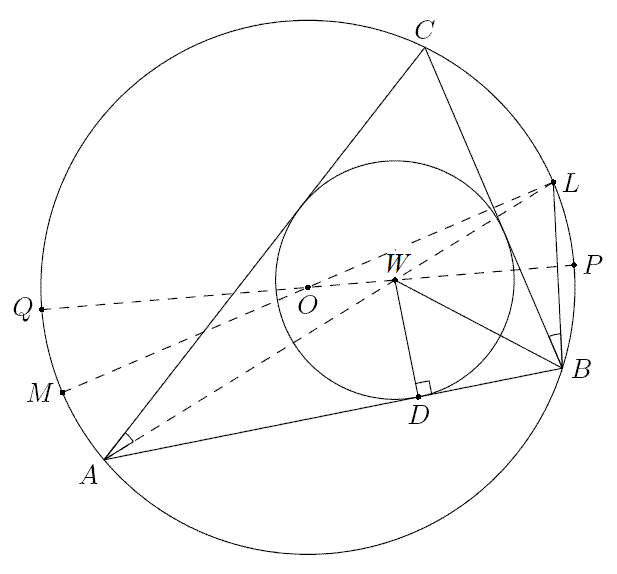
Jesteś tutaj
Organizatorzy konkursu
Patroni Konkursu
Kontakt Elektroniczny
sprawy techniczne:
konkurs_strona[at]mini.pw.edu.pl.
sprawy merytoryczne:
konkurs_uwagi[at]mini.pw.edu.pl.
reklamacje:
konkurs_odwolania[at]mini.pw.edu.pl.
Deklaracja Dostępności
Adres pocztowy
WYDZIAŁ MATEMATYKI I NAUK INFORMACYJNYCH POLITECHNIKI WARSZAWSKIEJ ul. Koszykowa 75, 00-662 WARSZAWA, pokój 17,
dopisek KONKURS
Wszystkie prawa zastrzeżone © 1999-2024 Wydział Matematyki i Nauk Informacyjnych Politechniki Warszawskiej
Stronę napędza Drupal