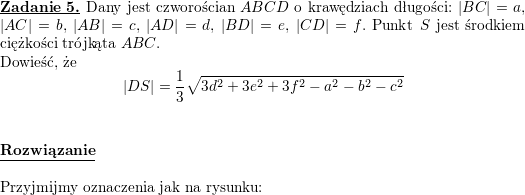Finał 2009 Rozwiązania

Wysłane przez dn w wt., 07/04/2015 - 21:59

$ \centerline{POWSZECHNY KONKURS INTERNETOWY dla uczniów szkół średnich - Matematyka} \centerline{Finał X edycji - 25 kwietnia 2009} \centerline{Przykładowe rozwiązania} $

$\textbf{\underline{Zadanie 1.}} Znaleźć wszystkie pary $(x,y)$ liczb rzeczywistych spełniające układ równań $$\left\{\begin{array}{l} \displaystyle \sqrt{\frac{x}{y}}+\sqrt{\frac{y}{x}}=\frac{7}{\sqrt{xy}}+1 \\ \\ x\sqrt{xy}+y\sqrt{xy}=78 \end{array}\right.$$ \\ \\ \textbf{\underline{Rozwiązanie}} \\ \\ Z pierwszego równania otrzymujemy, że $x,y$ muszą być tego samego znaku (i nie mogą być zerami). Jednak gdy rozważymy drugie równanie i przyjmiemy, że $x,y$ są ujemne, wtedy lewa strona równania będzie ujemna, a prawa dodatnia - sprzeczność. \\ Stąd wnioskujemy, że $x,y$ muszą być liczbami dodatnimi. \\ Pomnóżmy pierwsze równanie przez $\sqrt{xy}$: $$\left\{\begin{array}{l} x+y=7+\sqrt{xy} \\ \sqrt{xy}(x+y)=78 \end{array}\right.$$ \\ Podstawmy $u=x+y$, $v=\sqrt{xy}$ (oczywiście $u,v>0$): $$\left\{\begin{array}{l} u=7+v \\ uv=78 \end{array}\right.$$ $$(7+v)v=78$$ $$v^2+7v-78=0$$ $$(v-6)(v+13)=0$$ $$v=6\quad\vee\quad v=-13$$ \\ Ale $v>0$: $$\left\{\begin{array}{l} v=6 \\ u=13 \end{array}\right.$$ $$\left\{\begin{array}{l} \sqrt{xy}=6 \\ x+y=13 \end{array}\right.$$ $$\left\{\begin{array}{l} xy=36 \\ y=13-x \end{array}\right.$$ $$x(13-x)=36$$ $$x^2-13x+36=0$$ $$(x-4)(x-9)=0$$ \\ Dla $x=4$ mamy $y=9$ \\ Dla $x=9$ mamy $y=4$ \\ Rozwiązaniami są dwie pary: $(x,y)=(4,9)$, $(x,y)=(9,4)$. $

$\textbf{\underline{Zadanie 2.}} W trójkącie równoramiennym wysokości względem podstawy i ramienia mają długości $12$ cm i odpowiednio $14,4$ cm. Obliczyć stosunek promienia koła wpisanego w ten trójkąt do promienia koła na nim opisanego. \\ \\ \textbf{\underline{Rozwiązanie}} \\ \\ Przyjmijmy oznaczenia jak na rysunku: \\ $

$ Ponadto niech $|AB|=a$, $|BC|=b$, wtedy $|DB|=\frac{a}{2}$. \\ Z tw. Pitagorasa w $\Delta DBC$: $$\left(\frac{a}{2}\right)^2+12^2=b^2$$ $$b=\sqrt{144+\frac{a^2}{4}}$$ \\ Ponieważ $\Delta ABE\sim\Delta CDB$ (k-k-k), to: $$\frac{|AE|}{|AB|}=\frac{|CD|}{|CB|}$$ $$\frac{14.4}{a}=\frac{12}{\sqrt{144+\frac{a^2}{4}}}$$ \\ Stąd otrzymamy $a=18$, więc $b=15$. \\ Wtedy: $$P_{ABC}=\frac{1}{2}a\cdot 12=108$$ \\ Korzystając ze wzorów: $$P_{ABC}=\frac{(a+b+b)r}{2}\qquad P_{ABC}=\frac{abb}{4R}$$ \\ Gdzie $r,R$ to odpowiednio długości promieni okręgów wpisanego i opisanego: $$108=\frac{48r}{2}\qquad 108=\frac{18\cdot 15\cdot 15}{4R}$$ $$r=\frac{9}{2}\qquad R=\frac{75}{8}$$ \\ Więc szukany stosunek wynosi: $$\frac{r}{R}=\frac{12}{25}$$ $

$\textbf{\underline{Zadanie 3.}} W talii złożonej z $52$ kart jest po $13$ pików, kierów, kar i trefli. W każdym kolorze jest as, król, dama, walet i karty od dziesiątki do dwójki. W grze w pokera fulem nazywamy układ $5$ kart składający się z trzech kart tego samego typu oraz pary kart tego samego typu, np.: $3$ króle i $2$ asy. Wylosowanie dowolnych $5$ kart z tej talii jest tak samo prawdopodobne. Jakie jest prawdopodobieństwo wylosowania fula? \\ \\ \textbf{\underline{Rozwiązanie}} \\ \\ Niech $\Omega$ - oznacza wszystkie możliwości wylosowania pięciu kart z talii. \\ Oczywiście: $$|\Omega|={52\choose 5}$$ \\ Niech $A$ - oznacza wszystkie możliwości uzyskania fula. \\ Wtedy $\displaystyle |A|={13\choose 1}{4\choose 3}{12\choose 1}{4\choose 2}$. \\ Najpierw wybieramy jedną z trzynastu figur (od $2$ do asa), następnie z czterech kolorów dobieramy trzy, w ten sposób otrzymamy trzy karty, które utworzą nam część fula. Następnie wybieramy jedną z dwunastu pozostałych figur, a następnie z czterech kolorów dobieramy dwa. \\ \\ Stąd szukane prawdopodobieństwo jest równe: $$P(A)=\frac{|A|}{|\Omega|}=\ldots=\frac{4}{4165}$$ $

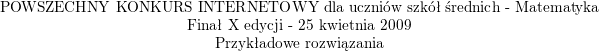
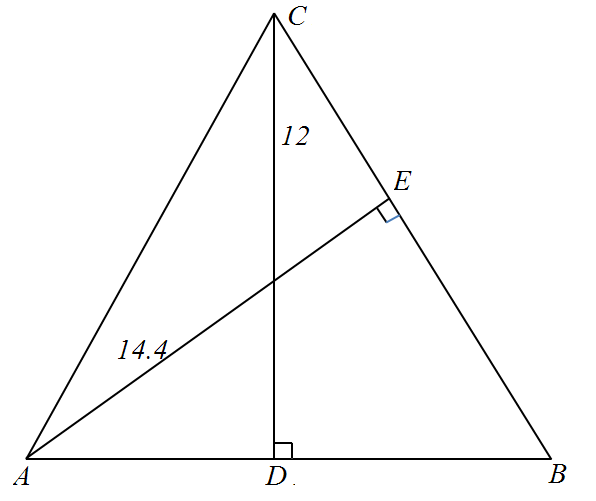
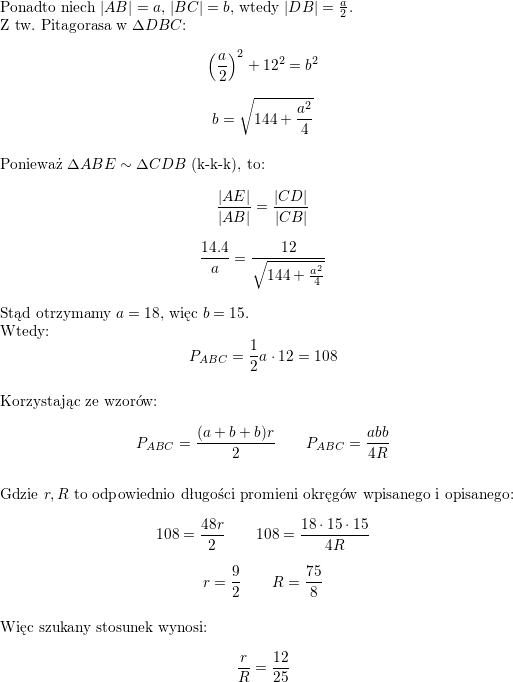
$\textbf{\underline{Zadanie 4.}} Wykazać, że liczba $$3\cdot 7\cdot 11\cdot 29\cdot 40\cdot 299\cdot\sin 10^{\circ}\cdot \cos 160^{\circ}\cdot \sin 130^{\circ}\cdot\left[\frac{1}{2}\log_{\frac{1}{2}}\left(2+\sqrt{3}\right)+\log_{\frac{1}{2}}\left(\sqrt{6}-\sqrt{2}\right)\right]$$ jest liczbą naturalną. Ile dzielników będących liczbami naturalnymi ma ta liczba? \\ \\ \textbf{\underline{Rozwiązanie}} \\ \\ Obliczmy (będziemy korzystać ze wzoru $\sin\alpha\cos\alpha=\frac{1}{2}\sin 2\alpha$ oraz ze wzorów redukcyjnych): $$\sin 10^{\circ}\cos 160^{\circ}\sin 130^{\circ}= \sin 10^{\circ}\cos (180^{\circ}-160^{\circ})\sin (90^{\circ}+40^{\circ})=$$ $$= -\sin 10^{\circ}\cos 20^{\circ}\cos 40^{\circ}= -\frac{\cos 10^{\circ}\sin 10^{\circ}\cos 20^{\circ}\cos 40^{\circ}}{\cos 10^{\circ}}=$$ $$= -\frac{\frac{1}{2}\sin 20^{\circ}\cos 20^{\circ}\cos 40^{\circ}}{\cos 10^{\circ}}= -\frac{\frac{1}{4}\sin 40^{\circ}\cos 40^{\circ}}{\cos ^{\circ}}=$$ $$= -\frac{\frac{1}{8}\sin 80^{\circ}}{\cos 10^{\circ}}= -\frac{\frac{1}{8}\cos 10^{\circ}}{\cos 10^{\circ}}= -\frac{1}{8}$$ \\ Ponadto: $$\frac{1}{2}\log_{\frac{1}{2}}\left(2+\sqrt{3}\right)+\frac{1}{2}\log_{\frac{1}{2}}\left(\sqrt{6}-\sqrt{2}\right)^2= \frac{1}{2}\left(\log_{\frac{1}{2}}\left(2+\sqrt{3}\right)+\log_{\frac{1}{2}}\left(6-2\sqrt{12}+2\right)\right)=$$ $$= \frac{1}{2}\left(\log_{\frac{1}{2}}(2+\sqrt{3})+\log_{\frac{1}{2}}(8-4\sqrt{3})\right)= \frac{1}{2}\log_{\frac{1}{2}}\left[(2+\sqrt{3})4(2-\sqrt{3})\right]=$$ $$= \frac{1}{2}\log_{\frac{1}{2}}4= \log_{\frac{1}{2}}2=-1$$ \\ Nasza liczba jest więc równa: $$M=3\cdot 7\cdot 11\cdot 29\cdot 8\cdot 5\cdot 13\cdot 23\cdot\left(-\frac{1}{8}\right)\cdot (-1)= 3\cdot 7\cdot 11\cdot 29\cdot 5\cdot 13\cdot 23$$ \\ Jako iloczyn liczb naturalnych liczba $M$ jest liczbą naturalną. \\ Liczbę $M$ przedstawiliśmy jako iloczyn siedmiu różnych liczb pierwszych. \\ By utworzyć dzielnik liczby $M$ musimy wybrać jakiś podzbiór z tych $7$ liczb pierwszych i wymnażając liczby z tego podzbioru utworzyć dzielnik (gdy wybierzemy zbiór pusty, przymijmy, że dzielnikiem jest $1$). Stąd ilość dzielników liczby $M$ jest równa ilości podzbiór zbioru $7$-elementowego, czyli $2^7=128$. $

$\textbf{\underline{Zadanie 5.}} Dany jest czworościan $ABCD$ o krawędziach długości: $|BC|=a$, $|AC|=b$, $|AB|=c$, $|AD|=d$, $|BD|=e$, $|CD|=f$. Punkt $S$ jest środkiem ciężkości trójkąta $ABC$. \\ Dowieść, że $$|DS|=\frac{1}{3}\sqrt{3d^2+3e^2+3f^2-a^2-b^2-c^2}$$ \\ \\ \textbf{\underline{Rozwiązanie}} \\ \\ Przyjmijmy oznaczenia jak na rysunku: $

$Skoro $S$ jest środkiem cięzkości trójkąta $ABC$, to jest to punkt przecięcia się środkowych w tym trójkącie. \begin{itemize} \item Popatrzmy na przekrój $BCD$, oczywiście $|BE|=\frac{a}{2}$. \\ Z tw. cosinusów w trójkątach: $BCD$ oraz $BED$ otrzymujemy układ równań: $$\left\{\begin{array}{l} |DE|^2=\frac{a^2}{4}+e^2-2\cdot\frac{a}{2}\cdot e\cos\alpha \\ f^2=a^2+e^2-2ae\cos\alpha \end{array}\right.$$ \\ Mnożymy pierwsze równanie przez $2$: $$\left\{\begin{array}{l} 2|DE|^2=\frac{a^2}{2}+2e^2-2ae\cos\alpha \\ f^2=a^2+e^2-2ae\cos\alpha \end{array}\right.$$ \\ Odejmujemy stronami: $$2|DE|^2-f^2=-\frac{a^2}{2}+e^2$$ $$|DE|^2=\frac{2e^2+2f^2-a^2}{4}$$ \item Popatrzmy na przekrój $BCA$, w analogiczny sposób wyznaczamy długość $|AE|$: $$|AE|^2=\frac{2b^2+2c^2-a^2}{4}$$ \item Popatrzmy na przekrój $AED$. Oczywiście $|AS|=\frac{2}{3}|AE|$ (środkowe przecinają się w jednym punkcie, który dzieli je w stosunku $2:1$, licząc od wierzchołka w trójkącie). \\ Analogicznie jak wcześniej stosujemy tw. cosinusów dla trójkątów $ASD$ oraz $AED$: $$\left\{\begin{array}{l} |DS|^2=d^2+\left(\frac{2}{3}\right)^2|AE|^2-2d\cdot\frac{2}{3}|AE|\cos\gamma \\ |DE|^2=d^2+|AE|^2-2d|AE|\cos\gamma \end{array}\right.$$ \\ Mnożymy pierwsze równanie przez $\frac{3}{2}$ i odejmujemy stronami równania: $$\frac{3}{2}|DS|^2-|DE|^2=\frac{1}{2}d^2-\frac{1}{3}|AE|^2$$ \\ Wykorzystując wcześniej obliczone wielkości $|DE|^2$ oraz $|AE|^2$ otrzymamy: $$|DS|^2=\frac{1}{9}(3d^2+3e^2+3f^2-a^2-b^2-c^2)$$ $$|DS|=\frac{1}{3}\sqrt{3d^2+3e^2+3f^2-a^2-b^2-c^2}$$ $