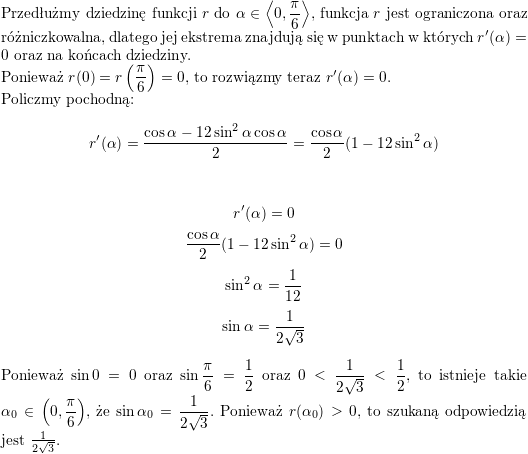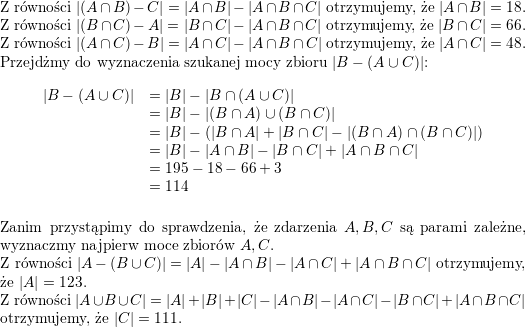Finał 2001 Rozwiązania

Wysłane przez dn w wt., 15/09/2015 - 12:36

$ \centerline{POWSZECHNY INTERNETOWY KONKURS dla uczniów szkół średnich - Matematyka} \centerline{Finał II edycji - 9 czerwca 2001} \centerline{Przykładowe rozwiązania} $

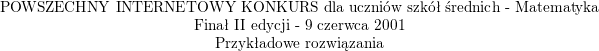
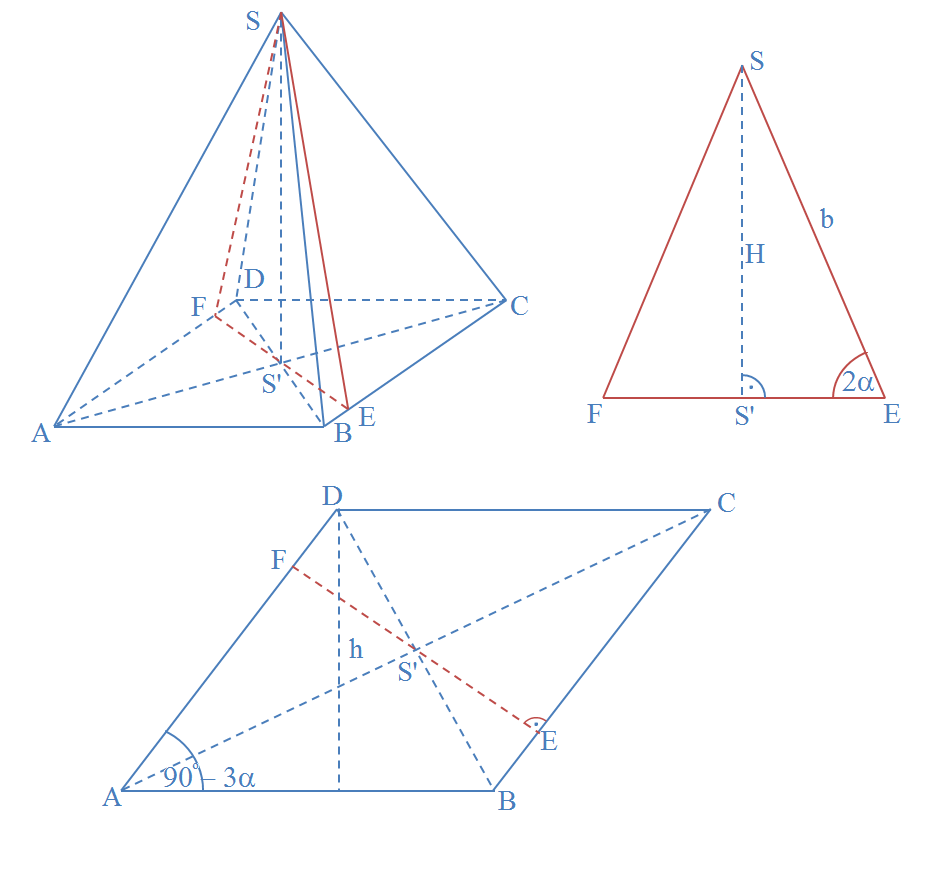
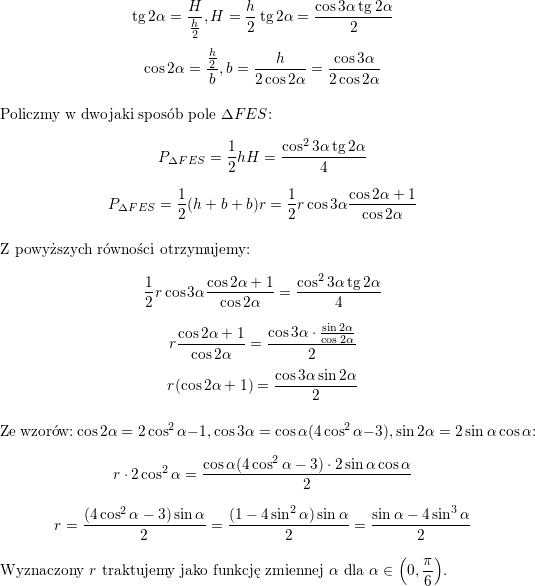
$\textbf{\underline{Zadanie 1.}} Wykazać, że liczby postaci $$\sqrt{\underbrace{1\ldots 1}_{n+1}\underbrace{5\ldots 5}_{n}6}$$ są całkowite dla każdej liczby naturalnej $ n$. \\ \\ \textbf{\underline{Rozwiązanie}} \\ \\ Zapiszmy w inny sposób liczbę pod pierwiastkiem: $$\begin{array}{l} \displaystyle \underbrace{1\ldots 1}_{n+1}\underbrace{5\ldots 5}_n6= \\ \\ \displaystyle =\underbrace{1\ldots 1}_{n+1}\cdot 10^{n+1}+\underbrace{5\ldots 5}_n\cdot 10+6=\\ \\ \displaystyle =\frac{1}{9}\cdot\underbrace{9\ldots 9}_{n+1}\cdot 10^{n+1}+\frac{5}{9}\cdot\underbrace{9\ldots 9}_n\cdot 10+6=\\ \\ \displaystyle =\frac{1}{9}\cdot (10^{n+1}-1)\cdot 10^{n+1}+\frac{5}{9}\cdot (10^n-1)\cdot 10+6=\\ \\ \displaystyle =\frac{1}{9}\left[(10^{n+1})^2-10^{n+1}+5\cdot 10^{n+1}-50+54\right]=\\ \\ \displaystyle =\frac{1}{9}\left[(10^{n+1})^2+4\cdot 10^{n+1}+4\right]=\\ \\ \displaystyle =\left[\frac{1}{3}\left(10^n+2\right)\right]^2 \end{array}$$ Ponieważ $\displaystyle 3\left|(10^{n+1}+2)\right.$ (np. dlatego, że suma cyfr liczby $10^n+2$ jest równa $3$), to udowodniliśmy, że dane w poleceniu liczby są liczbami całkowitymi dla każdej liczby naturalnej $n$. \\ \\ $

$\textbf{\underline{Zadanie 2.}} Funkcja $ F\left( x\right) $ spełnia warunki \\ \\ (i) $ F\left(1\right) =0$; \\ (ii) $ F\left( x\right) >0$ dla $ x>1$; \\ (iii)$ F^{\prime}\left( x\right) =\frac{1}{x}$ dla $ x\geq1$. \\ \\ Wyznaczyć wszystkie wartości parametru rzeczywistego $ a$, dla których nierówność $$\displaystyle F\left( x\right) >\frac{a\left( x-1\right) }{x+1}$$ jest prawdziwa dla każdego $ x>1$. \\ \\ \textbf{\underline{Rozwiązanie}} \\ \\ Pokażemy najpierw, że funkcja $F$ jest lewostronnie ciągła dla $x=1$, skoro wiemy, że $F'(x)=\frac{1}{x}$, to $F'_+(1)=1$, dalej z definicji pochodnej: $$\lim_{h\to 0^+}\frac{F(1+h)-F(1)}{h}=1$$ $$\lim_{h\to 0^+}\frac{F(1+h)}{h}=1$$ \\ By powyższa granica mogła wynosić $1$, to musi zachodzić $\displaystyle\lim_{h\to 0^+}F(1+h)=0$, zatem rzeczywiście funkcja $F$ jest lewostronnie ciągła dla $x=1$, zatem $F$ jest ciągła dla $x\geqslant 1$. \\ $ $ \\ Na początek zauważmy, że gdy $a\leqslant 0$, to nierówność jest w oczywisty sposób spełniona dla każdego $x>1$. \\ \\ Niech teraz $a>0$. \\ \\ Rozważmy funkcję $\displaystyle M(x)=F(x)-a\cdot\frac{x-1}{x+1}$ dla $x\geqslant 1$. Oczywiście $M(1)=0$ oraz $M$ jest ciągła. \\ Chcemy znaleźć te wartości $a$ dla których $M(x)>0$ dla każdego $x>1$. \\ Policzmy pochodną: $$M'(x)=\frac{1}{x}-a\cdot\frac{x+1-x+1}{(x+1)^2}=\frac{(x+1)^2-2ax}{x(x+1)^2}=\frac{x^2-2x(a-1)+1}{x(x+1)^2}$$ \\ Mianownik powyższego wyrażenia jest dodatni dla $x>1$. \\ Niech $\Delta_l$ oznacza wyróżnik trójmianu kwadratowego, będącego w liczniku pochodnej $M'(x)$. \begin{itemize} \item gdy $\Delta_l<0$, to oczywiście $M'(x)>0$ zatem $M(x)$ będzie funkcją rosnącą dla $x>1$, zatem dla każdego $x>1$ będzie zachodziło $M(x)>M(1)=0$. \\ Wyznaczmy zatem rozwiązanie nierówności $\Delta_x<0$: \end{itemize} $ $ $$4(a-1)^2-4<0$$ $$(a-1)^2<1$$ $$|a-1|<1$$ $$a\in(0,2)$$ \begin{itemize} \item Sprawdźmy co się dzieje, gdy $\Delta_l=0$, czyli $a\in\{0,2\}$. Przypadek $a=0$ już wcześniej rozważyliśmy, dla $a=2$ otrzymujemy: $\displaystyle M'(x)=\frac{(x-1)^2}{x(x+1)^2}$, zatem dla każdego $x>1$ mamy $M'(x)>0$, więc dla $x>1$ funkcja $M(x)$ jest funkcją rosnącą, czyli będzie zachodziło $M(x)>M(1)=0$. \item Gdy $\Delta_l>0$, to mamy dwa takie $x_1,x_2$ dla których zachodzi: $x_1+x_2=2(a-1)$ oraz $x_1x_2=1$. Skoro $x_1+x_2>0,x_1x_2>0$, to obydwa pierwiastki $x_1,x_2$ są dodatnie, a ponieważ $x_1x_2=1$, to jeden z tych pierwiastków jest mniejszy od $1$, a drugi większy. Niech $x_1<x_2$. Zatem w przedziale $x\in(1,x_2)$ mamy $M'(x)<0$, zatem w tym przedziale $M(x)$ jest malejąca, czyli dla $x\in(1,x_2)$ mamy nierówność $M(x)<M(1)=0$, zatem ten przypadek nie spełnia warunków postawionych w zadaniu. \\ \\ \end{itemize} Reasumując odpowiedź to $a\in\left(-\infty,2\right>$. \\ \\ $

$\textbf{\underline{Zadanie 3.}} Narysować zbiór punktów płaszczyzny, których współrzędne $ x$, $ y$ spełniają układ nierówności $$\left\{\begin{array}{l} 0<x<2\pi \\ 0<y<2\pi \\ \sin x<\sin y\end{array}\right.$$ \\ \\ \textbf{\underline{Rozwiązanie}} \\ \\ Rozważmy funkcję $f(x,y)=\sin x-\sin y$. Jest to funkcja ciągła, zatem zbiór tych $(x,y)\in\mathbb{R}^2$ dla których $f(x,y)=0$ dzieli nam płaszczyznę $\mathbb{R}^2$ na obszary dla których funkcja $f$ jest albo dodatnia, albo ujemna, albo równa $0$, nam chodzi o zaznaczenie tych obszarów dla których $f(x,y)<0$. \\ Rozwiążmy najpierw $f(x,y)=0$: $$\sin x=\sin y$$ $$y=x+2k\pi\quad\vee\quad y=\pi-x+2k\pi, k\in\mathbb{Z}.$$ \\ Wystarczy teraz po jednym punkcie z danych obszarów i obliczyć znak funkcji $f$, znak $f$ będzie taki sam na całym obszarze. Odpowiedzią będzie: $

$\textbf{\underline{Zadanie 4.}} Podstawą ostrosłupa jest romb o boku długości $ 1$ i kącie ostrym $ 90^{\circ}-3\alpha$. Ściany boczne ostrosłupa nachylone są do płaszczyzny podstawy pod kątem $ 2\alpha$. Obliczyć promień kuli wpisanej w ten ostrosłup. Znaleźć$ \sin\alpha$, dla którego promień kuli wpisanej jest największy. \\ \\ \textbf{\underline{Rozwiązanie}} \\ \\ $

$ \\ Z treści zadania otrzymujemy, że $\displaystyle\alpha\in\left(0,\frac{\pi}{6}\right)$. \\ Ponieważ każda ściana boczna jest nachylona do płaszczyzny podstawy pod takim samym kątem, to spodek wysokości znajduje się w środku okręgu wpisanego w podstawę, czyli na przecięciu się przekątnych rombu $ABCD$. \\ W rombie $ABCD$ zachodzi: $\displaystyle\sin(90^{\circ}-3\alpha)=\frac{h}{1}$, zatem $h=\cos 3\alpha$. \\ Poprowadźmy przekrój płaszczyzną zawierającą $\Delta FES$, wtedy promień okręgu wpisanego w ten trójkąt jest równy promieniowi kuli wpisanej w czworościan. \\ W $\Delta FES$: $ $ $$\tan 2\alpha=\frac{H}{\frac{h}{2}}, H=\frac{h}{2}\tan 2\alpha=\frac{\cos 3\alpha\tan 2\alpha}{2}$$ $$\cos 2\alpha=\frac{\frac{h}{2}}{b}, b=\frac{h}{2\cos 2\alpha}=\frac{\cos 3\alpha}{2\cos 2\alpha}$$ \\ Policzmy w dwojaki sposób pole $\Delta FES$: $$P_{\Delta FES}=\frac{1}{2}hH=\frac{\cos^23\alpha\tan 2\alpha}{4}$$ $$P_{\Delta FES}=\frac{1}{2}(h+b+b)r=\frac{1}{2}r\cos 3\alpha\frac{\cos 2\alpha+1}{\cos 2\alpha}$$ \\ Z powyższych równości otrzymujemy: $$\frac{1}{2}r\cos 3\alpha\frac{\cos 2\alpha+1}{\cos 2\alpha}=\frac{\cos^23\alpha\tan 2\alpha}{4}$$ $$r\frac{\cos 2\alpha+1}{\cos 2\alpha}=\frac{\cos 3\alpha\cdot\frac{\sin 2\alpha}{\cos 2\alpha}}{2}$$ $$r(\cos 2\alpha+1)=\frac{\cos 3\alpha\sin 2\alpha}{2}$$ \\ Ze wzorów: $\cos 2\alpha=2\cos^2\alpha-1$, $\cos 3\alpha=\cos\alpha(4\cos^2\alpha-3)$, $\sin 2\alpha=2\sin\alpha\cos\alpha$: $$r\cdot 2\cos^2\alpha=\frac{\cos\alpha(4\cos^2\alpha-3)\cdot 2\sin\alpha\cos\alpha}{2}$$ $$r=\frac{(4\cos^2\alpha-3)\sin\alpha}{2}=\frac{(1-4\sin^2\alpha)\sin\alpha}{2}=\frac{\sin\alpha-4\sin^3\alpha}{2}$$ \\ Wyznaczony $r$ traktujemy jako funkcję zmiennej $\alpha$ dla $\displaystyle\alpha\in\left(0,\frac{\pi}{6}\right)$. \\ $ $ \\ Przedłużmy dziedzinę funkcji $r$ do $\displaystyle\alpha\in\left<0,\frac{\pi}{6}\right>$, funkcja $r$ jest ograniczona oraz różniczkowalna, dlatego jej ekstrema znajdują się w punktach w których $r'(\alpha)=0$ oraz na końcach dziedziny. \\ Ponieważ $\displaystyle r(0)=r\left(\frac{\pi}{6}\right)=0$, to rozwiązmy teraz $r'(\alpha)=0$. \\ Policzmy pochodną: $$r'(\alpha)=\frac{\cos\alpha-12\sin^2\alpha\cos\alpha}{2}=\frac{\cos\alpha}{2}(1-12\sin^2\alpha)$$ \\ $$r'(\alpha)=0$$ $$\frac{\cos\alpha}{2}(1-12\sin^2\alpha)=0$$ $$\sin^2\alpha=\frac{1}{12}$$ $$\sin\alpha=\frac{1}{2\sqrt{3}}$$ \\ Ponieważ $\sin 0=0$ oraz $\displaystyle\sin\frac{\pi}{6}=\frac{1}{2}$ oraz $\displaystyle 0<\frac{1}{2\sqrt{3}}<\frac{1}{2}$, to istnieje takie $\displaystyle \alpha_0\in\left(0,\frac{\pi}{6}\right)$, że $\displaystyle\sin\alpha_0=\frac{1}{2\sqrt{3}}$. Ponieważ $r(\alpha_0)>0$, to szukaną odpowiedzią jest $\frac{1}{2\sqrt{3}}$. \\ \\ $

$\textbf{\underline{Zadanie 5.}} Wśród cech półfinalistów konkursu matematycznego wyróżniamy następujące cechy: \\ \\ $ A$ - uczestnicy korzystający z komputera przy rozwiązywaniu zadań, \\ $ B$ - uczestnicy mieszkający dalej niż 200 km od Warszawy, \\ $ C$ - uczestnicy płci żeńskiej. \\ \\ Wśród 300 półfinalistów 60 osób miało tylko cechę $ A$, 195 osób cechę $ B$, 15 osób tylko cechy $ A$ i $ B$, 63 osoby tylko cechy $ B$ i$ C$, 45 osób tylko cechy $ A$ i $ C$ oraz 3 osoby miały cechy $ A$, $ B$, i$ C$. Ile osób miało tylko cechę $ B$? \\ Oznaczmy przez $ A$,$ B$, $ C$ zdarzenia polegajace na tym, że uczestnik konkursu ma odpowiednio cechę $ A$, $ B$, $ C$. Wykazać, że zdarzenia $ A$, $ B$, $ C$ są parami zależne. \\ \\ \textbf{\underline{Rozwiązanie}} Z treści zadania wiemy, że: \begin{itemize} \item $|A\cup B\cup C|=300$, \item $|A-(B\cup C)|=60$, \item $|B|=195$, \item $|(A\cap B)-C|=15$, \item $|(B\cap C)-A|=63$, \item $|(A\cap C)-B|=45$, \item $|A\cap B\cap C|=3$. \\ \end{itemize} $ $ Z równości $|(A\cap B)-C|=|A\cap B|-|A\cap B\cap C|$ otrzymujemy, że $|A\cap B|=18$. \\ Z równości $|(B\cap C)-A|=|B\cap C|-|A\cap B\cap C|$ otrzymujemy, że $|B\cap C|=66$. \\ Z równości $|(A\cap C)-B|=|A\cap C|-|A\cap B\cap C|$ otrzymujemy, że $|A\cap C|=48$. \\ Przejdżmy do wyznaczenia szukanej mocy zbioru $|B-(A\cup C)|$: $$\begin{array}{ll} |B-(A\cup C)| & =|B|-|B\cap(A\cup C)| \\ & =|B|-|(B\cap A)\cup (B\cap C)|\\ & =|B|-\left(|B\cap A|+|B\cap C|-|(B\cap A)\cap (B\cap C)|\right)\\ & =|B|-|A\cap B|-|B\cap C|+|A\cap B\cap C|\\ & =195-18-66+3\\ & =114\end{array}$$ \\ Zanim przystąpimy do sprawdzenia, że zdarzenia $A,B,C$ są parami zależne, wyznaczmy najpierw moce zbiorów $A,C$. \\ Z równości $|A-(B\cup C)|=|A|-|A\cap B|-|A\cap C|+|A\cap B\cap C|$ otrzymujemy, że $|A|=123$. \\ Z równości $|A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|+|A\cap B\cap C|$ otrzymujemy, że $|C|=111$. $ $ \\ Teraz by pokazać, że zdarzenia $A,B,C$ są parami zalezne wystarczy pokazać, że nie zachodzą równości $P(A)P(B)=P(A\cap B)$, $P(A)P(C)=P(A\cap C)$, $P(B)P(C)=P(B\cap C)$. \begin{itemize} \item $$P(A)P(B)=P(A\cap B)$$ $$\frac{|A|}{|A\cup B\cup C|}\cdot\frac{|B|}{|A\cup B\cup C|}=\frac{|A\cap B|}{|A\cup B\cup C|}$$ $$\frac{123}{300}\cdot\frac{195}{300}=\frac{18}{300}$$ $$123\cdot 195=18\cdot 300$$ Powyższa równość nie zachodzi, ponieważ lewa strona jest liczbą nieparzystą, a prawa parzystą, dlatego zdarzenia $A$ i $B$ są zdarzeniami zależnymi. \item $$P(A)P(C)=P(A\cap C)$$ $$\frac{123}{300}\cdot\frac{111}{300}=\frac{48}{300}$$ $$123\cdot 111=48\cdot 300$$ Powyższa równość nie zachodzi, ponieważ lewa strona jest liczbą nieparzystą, a prawa parzystą, dlatego zdarzenia $A$ i $C$ są zdarzeniami zależnymi. \item $$P(B)P(C)=P(B\cap C)$$ $ $ $$\frac{195}{300}\cdot\frac{111}{300}=\frac{66}{300}$$ $$195\cdot 111=66\cdot 300$$ Powyższa równość nie zachodzi, ponieważ lewa strona jest liczbą nieparzystą, a prawa parzystą, dlatego zdarzenia $B$ i $C$ są zdarzeniami zależnymi. \\ \end{itemize} Poniżej diagram Venna prezentujący przedstawioną w zadaniu sytuację: $

$ \centerline{\bf Za rozwiązanie każdego zadania można uzyskać maksymalnie 20 punktów} $