Jesteś tutaj
Organizatorzy konkursu
Patroni Konkursu
Kontakt Elektroniczny
sprawy techniczne:
konkurs_strona[at]mini.pw.edu.pl.
sprawy merytoryczne:
konkurs_uwagi[at]mini.pw.edu.pl.
reklamacje:
konkurs_odwolania[at]mini.pw.edu.pl.
Deklaracja Dostępności
Adres pocztowy
WYDZIAŁ MATEMATYKI I NAUK INFORMACYJNYCH POLITECHNIKI WARSZAWSKIEJ ul. Koszykowa 75, 00-662 WARSZAWA, pokój 17,
dopisek KONKURS
Wszystkie prawa zastrzeżone © 1999-2024 Wydział Matematyki i Nauk Informacyjnych Politechniki Warszawskiej
Stronę napędza Drupal

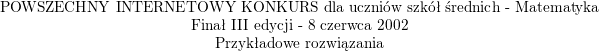
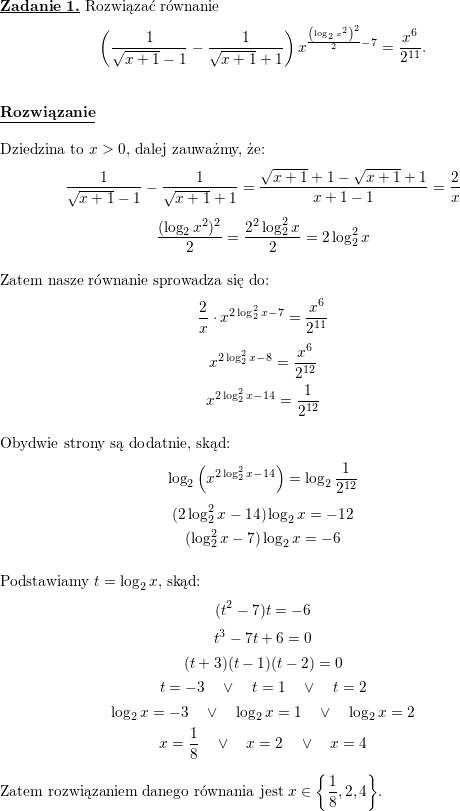



![<br />
\\ Oczywiście $x>0$<br />
\begin{itemize}<br />
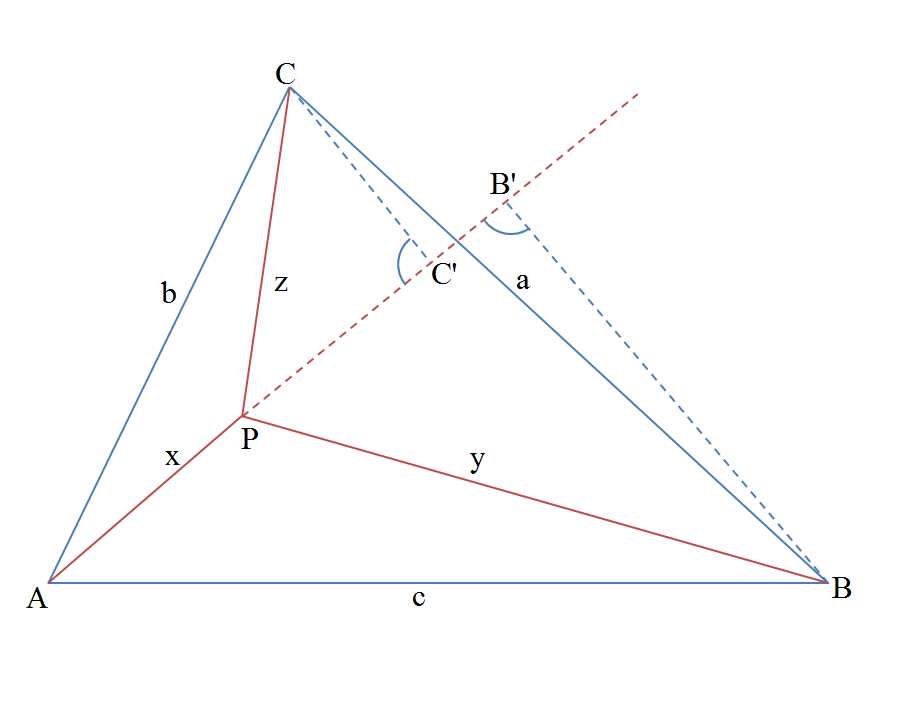
\item Gdy $x\in\left(0,2R\right>$, to pole danej części przekroju jest równe polu prostokąta o bokach długości $R$ oraz $x$, zatem $S(x)=Rx$.<br />
\item Gdy $x\in\left(2R,3R\right>$, to pole danej części przekroju jest równe polu prostokąta o bokach długości $R$ oraz $2R$, oraz polu równoległoboka, które obliczymy w następujący sposób: od pola trójkąta o podstawie $2R$ i wysokości $R$ odejmiemy pole trójkąta o podstawie $2\cdot [R-(x-2R)]=2(3R-x)$ oraz o wysokości $R-(x-2R)=3R-x$, zatem:<br />
$$S(x)=R\cdot 2R+\frac{1}{2}\cdot 2R\cdot R-\frac{1}{2}\cdot 2(3R-x)(3R-x)=-(x-3R)^2+3R^2$$<br />
\item Gdy $x>3R$, to pole danej części przekroju jest równe polu prostokąta o bokach $R,2R$ oraz polu trójkąta o podstawie $2R$ i wysokości $R$, zatem:<br />
$$S(x)=R\cdot 2R+\frac{1}{2}\cdot 2R\cdot R=3R^2$$<br />](/files/tex/138f2ff337eb58c8d4d6511906184e3426046848.png)